Why Array Index starts with 0 and not 1?

I’ve been coding for quite a few years, developing products and building projects, and I can’t even count how many times I’ve used arrays. They’re one of the data structures a developer usually works with. Yet, not once did it occur to me to ask: why does the array index always start from 0 and not 1? Wouldn’t it be simpler and less complex?

Well, if you have also thought about it then welcome to the curious club, and if you already know the answer then congratulations on getting 1 step closer to becoming a better engineer!

To get to the answer, we first need to cover some basics of arrays and memory allocation. While there won’t be any code written in this blog, I’ll be using C++ for the examples. But don’t worry — I’ll explain everything in the clearest way possible.

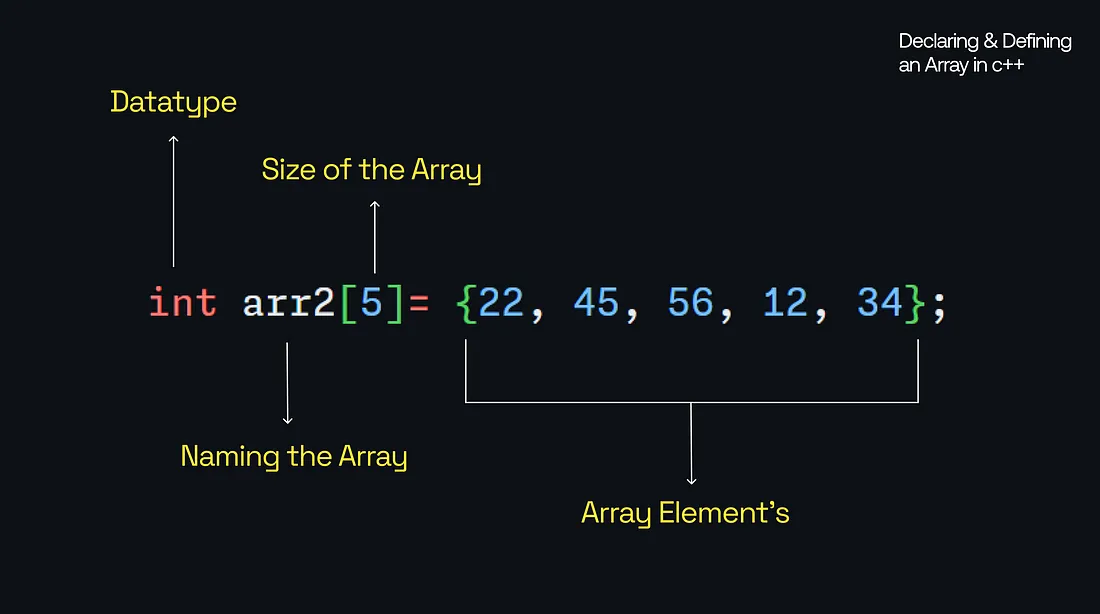
In the image below, I’ve shown how I declared an array in C++. I picked C++ because it helps explain the basics clearly. The array is named ‘arr2’. If you’re someone who hasn’t worked with statically-typed languages like C++ or Java, you might not realize that in these languages, you have to specify the datatype when declaring a variable. This applies to arrays as well.

In my example, I created an array to hold integer values, so I set the datatype to ‘int’. The size of the array [5], tells the machine to create an array that can store 5 integer values. If I wanted to store 10 values, it would be arr2[10], and for 1,000 values arr2[1000]. Finally, we declare the actual values inside curly braces.

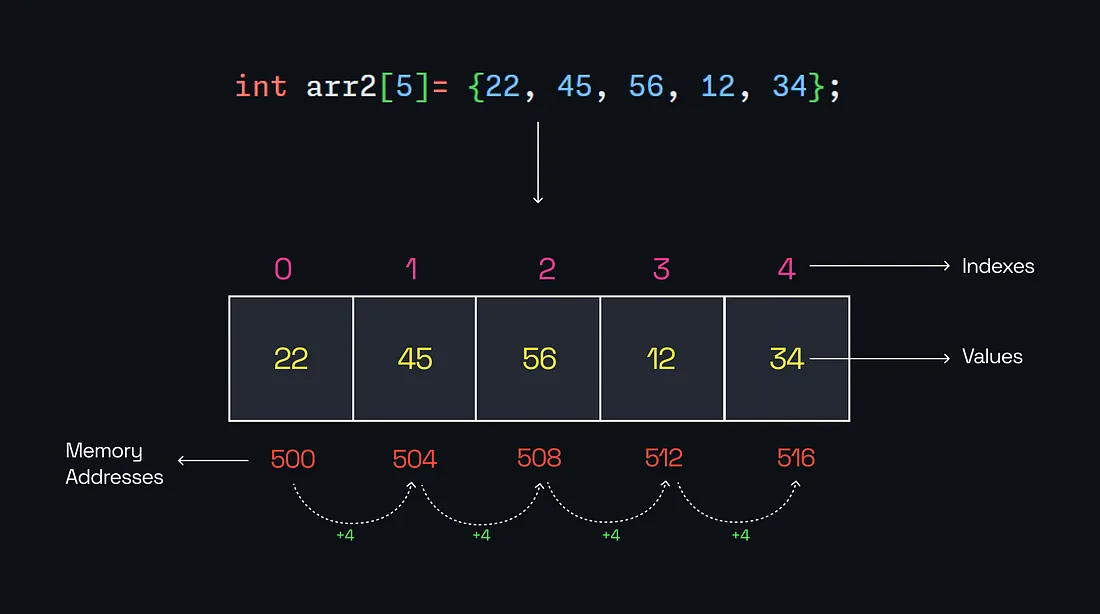
Understanding How Arrays Store Values in Memory

I know that the above Image may confuse you but don’t worry I will explain everything in Detail. Now one of the basic definition of an Array is that it stores values at contiguous locations. Now you are again confused I know but as I said don’t worry!

After we declare the array, the machine takes our Input and creates an array as per our definition. Each element of the array occupies a fixed number of bytes, depending on the data type. For instance:

• In most systems, an integer (int) typically takes 4 bytes.
• Character (char) typically takes 1 byte.
• float (float) typically takes 4 bytes.

In our example, we have declared the datatype as an Integer (int), which means each value in the array will occupy 4 bytes of memory. As mentioned earlier, an array stores its values in contiguous memory locations. This means all the values are placed sequentially, one after another, rather than being scattered across different, far-apart locations. But why is this important?

Why is Storing Array Values in Scattered Memory Locations Inefficient?

Imagine if the values of an array were stored at random or scattered memory locations, as illustrated in the diagram. While it’s technically possible for the machine to allocate these random locations and later access the values, this approach introduces several inefficiencies — especially when retrieving the values.

The inefficiencies don’t arise when assigning values to memory locations but become evident during retrieval. Let’s consider an example:

Suppose you define an array with 1000 values, and the computer stores these values in random memory locations. Now, you execute a command to retrieve and print all the array values. To do so, the computer would need to fetch each value from its respective random location, one by one.

Here’s where the problems arise:

• Retrieval Overhead: The computer must locate each value using complex algorithms, significantly increasing time and computational effort.
• Performance Bottleneck: Scattered locations disrupt sequential access, forcing multiple lookups and slowing down the process.
• Scaling Issues: As array size grows, inefficiencies multiply, causing substantial delays for larger datasets, which is unacceptable for optimized applications.

Why Contiguous Memory is Preferred?

Storing array values in contiguous memory locations allows the computer to calculate and access any element’s address directly using simple arithmetic, eliminating the need for complex lookups. This ensures faster retrieval, efficient use of cache memory, and seamless iteration, making it highly optimized for performance — especially for large datasets.

Now the formula that is used to retrieve the memory location of any particular value from an Array is very simple:

Address =Base Address + (index of the element × Size of Each Element)

Yes, that’s it! I know, too many jargons, right? I will simplify it for you!

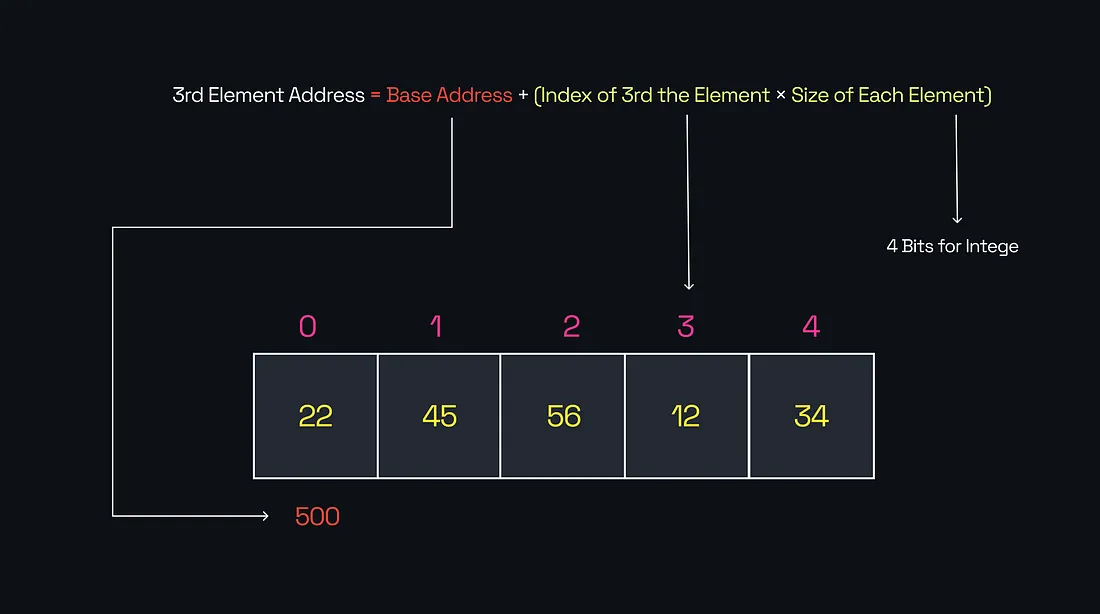
In the above image, what we are trying to do is to get the Memory address of the 3rd Element in the Array. Now to do that, we need 3 things:

• Base Address: This is where the first element of the array (index 0) is stored. In our case, the first element of that Array, which is 22, is stored in the memory location 500.
• Index ($i$): This tells us which element in the array we want to access. For example, $i = 2$ refers to the third element since array indexing starts at 0.
• Size of Each Element: Each element in the array takes up a fixed amount of memory, depending on the datatypes. For instance:
  • An int typically takes 4 bytes.
  • A char takes 1 byte.
  • A float takes 4 bytes.

Now, to find the memory address of the element at index 2:

500 + (2 × 4)=500 + 8 = 508

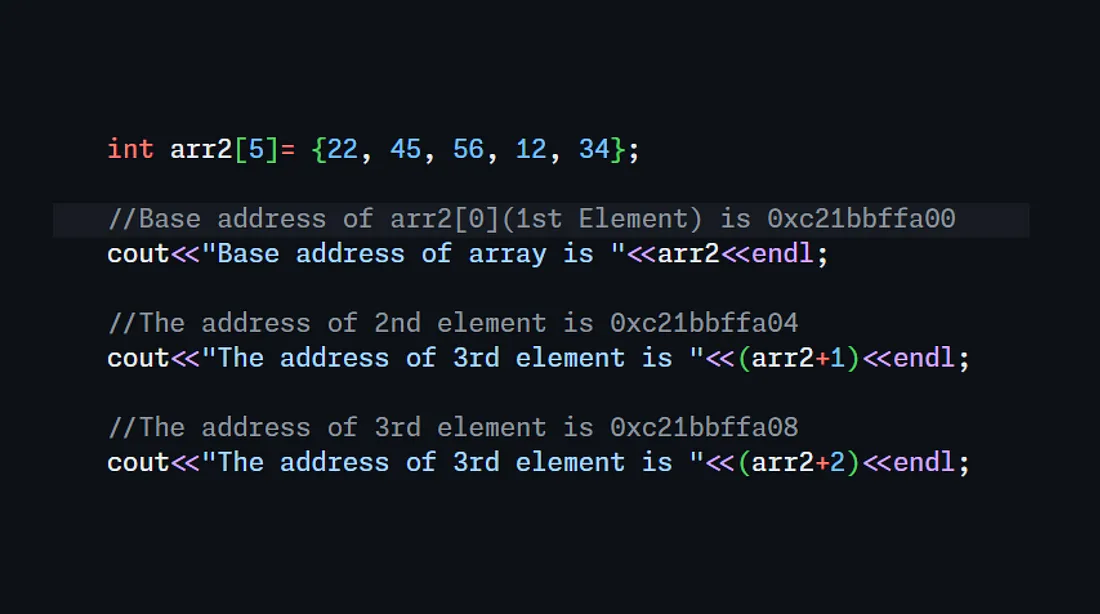
In the above image, you can see that the base address of the array (the address of the first element) is printed as 0xc21bbffa00. Notice the ending of the address: a00.

Now, when I printed the address of the second element, it shows 0xc21bbffa04. This is exactly 4 bytes more than the first element’s address.

Why? Because the size of each integer in the array is 4 bytes, and memory is allocated sequentially. Similarly, the address of the third element is 0xc21bbffa08, which is another 4 bytes ahead of the second element.

This demonstrates how array indexing works with memory:

• The index 0 corresponds to the base address (first element).
• The index 1 corresponds to the base address plus 4 bytes.
• The index 2 corresponds to the base address plus 8 bytes, and so on.

This sequential allocation is the reason why indexing starts from 0 — it directly maps to the memory offset, keeping calculations simple and efficient.

Why Starting Index from 1 Would Be Inefficient?

Now that we understand how memory addresses for array elements are calculated, let’s address the key question: why does the index start from 0 and not 1?

When an array is stored in memory, the first element is placed right at the base address of the array. For example, if the base address of the array is 500, the first element is stored there. Now, to calculate the memory address of any element, we use the formula:

Address = Base Address + (Index × Size of Each Element)

Here’s where the concept of distance comes in:

• The first element is at zero distance from the base address because it starts exactly where the array begins. That’s why its index is 0.
• The second element is at a distance of one element from the base address, so its index is 1, and so on.

By starting the index from 0, this relationship between distance and index becomes natural.

Now, imagine if indexing started at 1 instead. While the first element would still sit at the base address, its distance from the base address would not match its index anymore. To fix this mismatch, we’d have to subtract 1 from the index in every calculation. The formula would become:

Address = Base Address + ((Index — 1) × Size of Each Element)

For example: First element: 500 + ((1–1) × Size) = 500

This extra subtraction step adds unnecessary complexity and slows down memory access, especially for larger datasets. Starting the index from 0 eliminates this issue because the index directly represents the element’s distance from the base address.

To wrap things up, I hope this explanation helped you understand the concept of array indexing more clearly. I know it was a bit of a long read, but if it managed to add even a little to your knowledge, then I’ll consider this effort worthwhile.

Thank you for sticking through till the end — your curiosity and willingness to learn are what makes this journey so rewarding. Keep exploring, keep coding, and remember that every byte of knowledge brings you closer to mastering the art of programming!